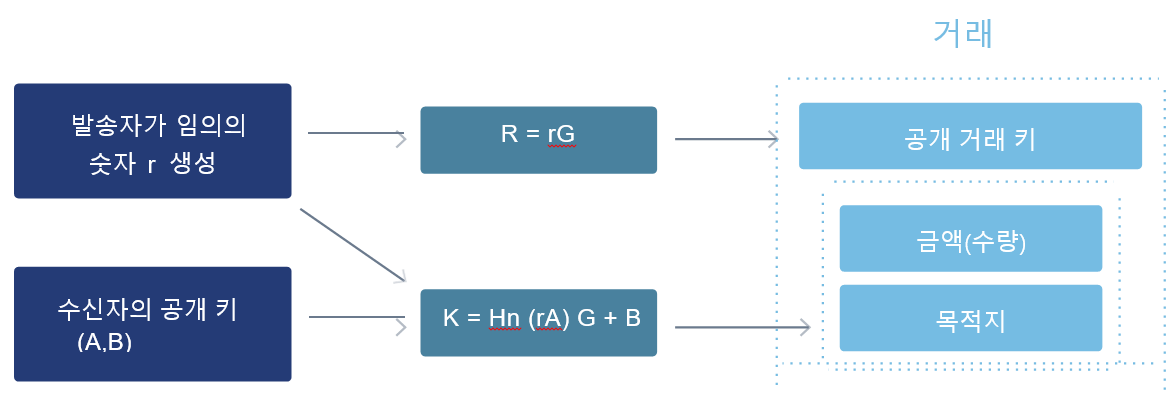
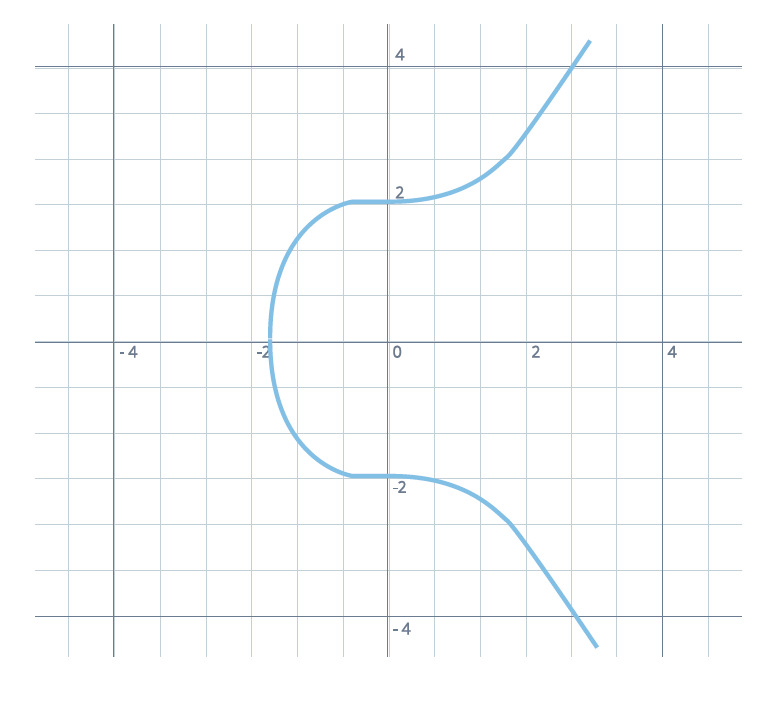Quras는 영지식 증명이라는 “zk-SNARK”를 사용합니다. zk-SNARK를 사용하면 거래와 스마트 컨트랙에서 완전한 프라이버시 (익명성)을 실현할 수 있습니다. zk-SNARK는 “Zero-Knowledge Succinct Non-Interactive Argument of Knowledge”(간결한 비상호작용적 영지식 증명)의 약자입니다. 간결함은 메시지 크기가 실제로 실행될 계산량보다 훨씬 작은 것을 의미합니다. 비상호적은 검증자와 승인자 간의 실시간 통신 없이도 검증이 가능함을 의미합니다. 지식의 논증은 계산에 의한 지식 검증을 말한다. 송금인, 송금 및 금액 정보를 숨기기 위해 zk-SNARK 기술을 사용하더라도 거래를 확인할 수 있는 세 가지 주요 알고리즘이 있습니다.

G: 키를 생성하는 알고리즘 (증명 키(pk) 및 검증 키(vk)는 특정 비밀 값 R과 프로그램 C (pk, vk)= G(R,C)으로 생성됨)

P: 증명은 검증 수행을 위한 검증자에서 알고리즘(증명 키 (pk))에 대한 입력 (h) 및 (X) prf = P(pk, X, h)를 검증하기 위한 정보로 생성

V: 입력 (h)과 증명 (prf)에서 검증이 올바른지 여부와 프로그램 C를 검증하는 알고리즘 (검증 키 (vk))까지 "옳음 또는 틀림"이 반환됨. V (vk, h, prf) = 참 또는 거짓. 이 작업의 목적은 승인자가 질문자에게 질문하지 않고 짧은 시간에 적은 계산량으로 검증 작업을 수행하는 것입니다.

zk-SNARK를 실행하려면 아래 단계가 필요합니다:

계산 연산 회로 R1CS QAP zk-SNARK

연산 회로

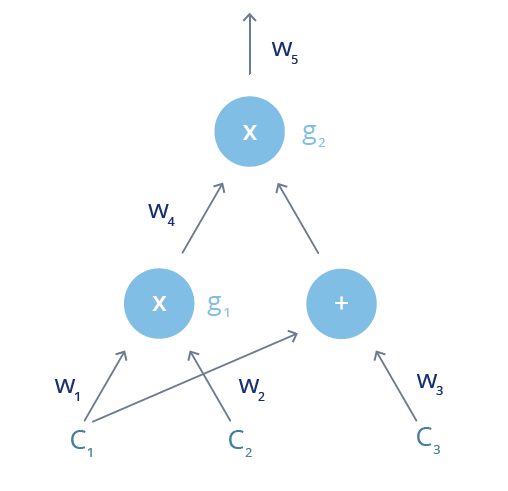
거래 효율적인 함수를 수학 식으로 변환하기 위해 논리적 단계를 가능한 한 최소 연산으로 분류하여 "산술 회로"를 만듭니다. A가 (c1 ˙ c2) ˙ (c1 + c3) = 7 인 것으로 c1, c2, c3가 알려 있을 때 c1, c2, c3의 값은 B에 표시되지 않고 c1, c2, c3가 알려져 있음을 증명합니다. , 첫 번째 단계는 산술 회로로 수학 공식을 표시하는 것입니다.

산술 회로는 게이트, 덧셈 및 곱셈을 연결하는 와이어와 같은 게이트 계산 연산자로 표현됩니다. 회로는 아래의 수학 공식과 같습니다:

R1CS:

다음으로, 산술 회로가 랭크 1 제약 시스템 (R1CS)으로 변환됩니다. R1CS는 3 개의 벡터 (a, b, c)로 이루어진 그룹의 시퀀스입니다. R1CS의 솔루션은 벡터 s를 만족시켜야 하며, 여기서 s는 s.a * s.b - s.c = 0. 방정식을 충족해야 합니다. s는 모든 벡터, 즉 [C1 , C2 , C3 , S1 , S2 , S3]을 나타냅니다. 이는 가상 변수 "one"을 추가함으로써 동일한 방법으로 추가 게이트를 표현할 수 있기 때문에, s 벡터는 [one, C1 , C2 , C3 , S1 , S2 , S3]가 됩니다. 이 세 개의 관문은 다음과 같습니다:

a=[0,1,0,0,0,0,0]
b=[0,0,1,0,0,0,0]
c=[0,0,0,0,1,0,0]
a=[1,0,0,0,0,0,0]
b=[0,1,0,1,0,0,0]
c=[0,0,0,0,0,1,0]
a=[0,0,0,0,1,0,0]
b=[0,0,0,0,0,1,0]
c=[0,0,0,0,0,0,1]

QAP:
다음 단계는 이 R1C를 QAP (Quadratic Arithmetic Programs) 형식으로 변환하는 것입니다. 위의 세 벡터 그룹은 x로 표현 된 행렬 a (x), b (x), c (x)를 표시 할 수 있습니다. P(x)=T(x)*H(x)가 증명되면 P(x)=s.a(x) * s.b(x) - s.c(x) , P(x)=T(x)*H(x) 로 표시되는 다항식이 존재합니다. s.a(x)를 L(x)로, s.b(x)를 R(x)로, s.c(x)를 O(x)로 정의함으로써 증명되어야 할 수학 공식은 L(x)*R(x)-O(x) =T(x)*H(x)로 다시 쓸 수 있습니다.

1. A는 위의 방법에 따라 다항식 L, R, O, H를 선택한다.
2. B는 임의의 점 s를 선택하고 E(T(s))를 계산한다.
3. A는 B에서 보낸 E(s2),...)을 기준으로 E(L(s)),E(R(s)),E(O(s)),E(H(s))를 계산한다.
4. B는 E(L(s)* R(s)-O(s))= E(H(s)* T(s))를 확인한다.

준동형 암호화라는 이론을 적용합니다. 준동형 암호화는 숫자 x, 또는 E(x)가 다음 성질을 만족시키는 함수로 정의합니다:

거의 모든 x에 있어서, 일단 E(x)가 발견되면 그것을 찾기가 어렵습니다. 입력이 다를 경우 출력도 달라집니다. 이는 x≠y의 경우 E(x)≠E(y)가 됨을 의미합니다.E(x)와 E(y)를 아는 사람이 있으면 E(x)와 E(y) E를 사용하여 (x + y)를 계산할 수 있습니다. 이것은 x와 y가 숨겨져 있는 동안 다른 사람들이 x + y의 결과를 알고 있다는 것을 증명할 수 있다는 것을 의미합니다.

zk-SNARK 기술을 사용하여 Quras 플랫폼에서 트랜잭션을 익명화할 수 있습니다. 자금을 송수신하는 동안 zk-SNARK 기술을 사용하여 다음과 같은 3 종류의 거래가 가능합니다: 1) 사설(스텔스 주소에서 스텔스 주소로), 2) 비공개 해제(스텔스 주소에서 공개 주소로) 및 3) 비공개 (공개 주소에서 스텔스 주소로).
비공개 (공개 주소에서 스텔스 주소로)
이는 zk-SNARKs를 사용하여 송신자, 수신자, 거래금액을 포함한 거래내역의 암호화를 의미합니다. 이를 사용하면 컨센서스 노드에서 사용자의 개인 키를 모르고도 암호화된 트랜잭션이 올바른지 여부를 결정할 수 있습니다.

zk-SNARK 거래

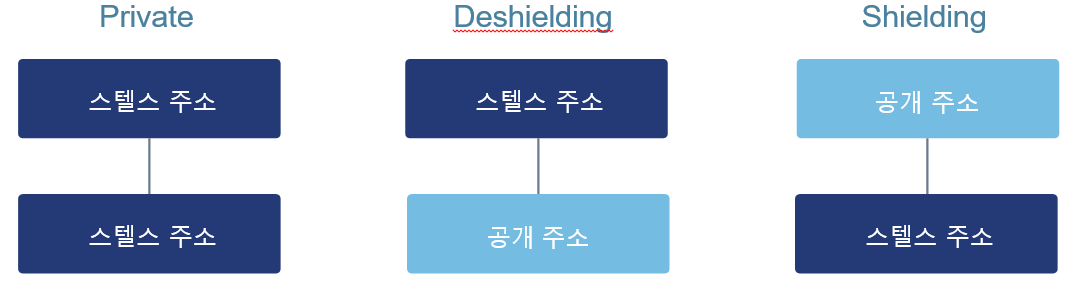
즉, zk-SNARKs – Commitment (커미트먼트, 확약) 및 Nullifier(무효화) 사용에는 두 가지 새로운 개념이 있습니다. QURAS 블록 체인에서 암호화 된 나머지 잔액이 노트(Note)로 표시된다고 가정하면 비트코인에서 노트의 개념은 UTXO의 유사한 개념으로 볼 수 있습니다. 차이점은 UTXO처럼 노트가 암호화 되어있어 투명성이 없다는 것입니다. 다음은 Verifier가 노트를 확인하는 방법을 설명합니다. Commitment는 비사용 노트(Unspent Note)로 간주될 수 있지만 비트코인의 경우 비사용 UTXO와 동일합니다.
Nullifier는 중복 지불 방지를 위해 사용할 수 있지만 이는 사용된 노트(Spent Note) 입니다. 거래로 입력 된 참조는 해시를 Nullfiler로 설정하여 게시됩니다. 거래 출력은 해시값이며 Commitment는 블록 체인에 게시됩니다. QURAS 블록체인에서 zk-SNARK를 사용하려면 먼저 다음 키가 생성됩니다:

VAmount_Old 및 VAmount_New의 값은 1 이상이 될 수 없습니다. 이 두 값이 모두 1 이상이면 트랜잭션은 실패로 간주됩니다. 또한, JoinSplit 증명 및 zk-SNARK 검증 키가 있어도 zk-SNARK 검증은 수행됩니다. True이면 트랜잭션은 성공한 것으로 간주됩니다. True가 아니면 트랜잭션은 실패로 간주됩니다.

암호화된 거래는 최소한 1개의 JoinSplit 항목을 포함해야 합니다. JoinSplit가 구축될 때 시그니처 키(JoinSplitSig)에 대한 키 쌍을 1단계에서 생성하여 JoinSplit을 검증해야 합니다. JoinSplit 생성이 완료되면 JoinSplitPrivKey를 사용하여 JoinSplit 바디에 서명합니다. 이 후, 블록체인 방송을 위한 거래를 생성하기 위해 거래에 JoinSplitSig를 입력합니다.

(노트 커미트먼트 트리의 깊이가 머클 뎁스(MerkleDepth)라고 가정.)
Quras 블록체인에서, 머클 트리의 Auth Path 이론을 기반으로 머클 트리의 루트 값과 정확성을 검증할 수 있습니다.

앞에서 언급한 바와 같이 익명 거래에는 JoinSplit 항목이 있습니다. JoinSplit 항목의 VAmount_old는 공개 잔고 풀에서 코인 인출을 의미합니다. VAmount_new는 공개 잔고 풀에 코인을 입금하는 것을 의미합니다. 사용자는 JoinSplit의 VAmount_old와 VAmount_new를 통해 Quras 블록체인의 전체 공개 잔액 풀의 잔금만 확인할 수 있습니다. 다른 해당 계정의 잔고는 볼 수 없습니다.

JoinSplit 항목은 2개 이상 있으며, 블록체인에 거래가 들어가면 JoinSplit의 커미트먼트가 블록체인의 노트 커미트먼트 머클 트리에 추가됩니다.
또한, JoinSplit의 Nullifier가 블록체인에 등록됩니다. 익명 거래를 등록할 때 Tx의 Nullifier가 이미 블록체인에 등록된 경우 거래가 이중 지출로 인식되어 2회 등록이 되지 않고 블록체인으로 반환됩니다.
Nullifer 계산에서, 노트에 임의의 문자열이 입력되더라도 그의 Nullifier 값은 다릅니다. 이런 방법으로 Nullifier는 이중 지출을 방지합니다.

스마트 컨트랙은 자발적으로 계산이 검증될 수 있음을 의미합니다. 토큰 거래의 프라이버시를 보호하기 위한 zk-SNARK 기술의 사용과 함께, 이는 검증 가능하고 익명화 된 계산을 수행하는 것이 가능합니다.

zk-SNARK의 증명 생성 및 검증은 특정 비밀 값 R 및 프로그램 C로부터 생성 된 증명 키 (pk) 및 검증 키 (vk)를 요구합니다. 이 R은 독성 폐기물이라고 합니다. Quras의 독성 폐기물은 신뢰할 수 있는 다중 당사자로부터 생성되며 완전히 폐기됩니다.

링 서명은 QURAS에서 사용되는 두 번째 익명 기술입니다. QURAS는 서명 후 문제가 발생할 경우 서명을 식별하는데 필요하기 때문에 관리자에게 링 서명 기술을 사용합니다.

서명자 공개 요청에는 2가지 유형이 있습니다: 1) 서명자가 링 서명이 자신임을 제3자 또는 당사자들에게 증명하는 서명자, 2) 주어진 서명의 익명성을 포기하고 서명자의 협조 없이 서명자를 식별하는 신뢰받는 관리자.

일회성 주소:

QURAS 블록체인에 대한 링 서명의 일회성 주소에는 이중 타원 곡선에서 생성 된 키 쌍 ((a, A) 및 (b, B))이 포함됩니다. 주소는 (A, B)에서 생성됩니다. (a, b)는 비밀 키입니다. (a, B)는 보기 키입니다. 자금 송금 절차는 아래를 참조하십시오:
• 1, 앨리스가 밥에게 자금을 보내려면 먼저 밥의 공개 키 (A, B)를 가져옵니다. • 2, 다음에 앨리스는 1< r< N인 임의의 r을 선택하여 일회용 공개 키 K = Hn(rA)G+B를 계산합니다. • 3, 앨리스는 K를 수신자로 설정하고, 거래 데이터에 R=rG 값을 추가하여 네트워크에 보냅니다. R=rG 값은 수신자가 Diffie-Hellman와 같은 공유 비밀을 계산하는데 사용됩니다. • 4, 밥은 데이터를 수신하고, R을 사용하여 aR=arG = rA 및 K' = Hn(aR)G + B를 계산합니다. aR=arG=rA 이고 K'= K이므로, 밥이 주소를 보면 자신의 주소임을 인식할 수 있습니다. • 5, 밥은 k=Hn(aR)+b를 사용하여 일회성 공개 키 K의 비밀 키를 복구할 수 있습니다. 그는 송금을 수행하기 위해 k를 사용하여 거래에 다시 서명합니다.

링 서명

QURAS 내에서 링 서명 거래 금액 정보를 숨기려면 다음과 같은 방법이 사용됩니다.:
b의 양은 C(b) = xG + bH로 정의되는 반면 x는 블라인딩 계수입니다.
만일 a1,...,an의 입력과 b1,...,bm의 출력으로 거래가 이루어진다면 관찰자는 당연히 다음을 기대할 것입니다:

커미트먼트는 가산적이므로 총계도 0 이 됩니다:

이는 거래의 송금인이 이전에 받은 코인보다 더 많은 동전을 보내지 않았음을 네트워크를 이용하여 확인하는 것입니다. 한편, 송금인의 신분이 확인되는 것을 피하기 위해, 커미트먼트는 0 이 아닌 구체적인 숫자가 되어야 합니다.

a, b, z에 대한 커미트먼트가 있고, 이를 사용하여 a + b = z임을 증명하는 경우, a = 3, b = 2, z = 5일 때 기본 자료가 Z7이면, a = 4, b= 5, z = 2 (mod7)에 적용할 수 있습니다. 이 문제를 해결하려면, a 값에 대해 풀기 위해, 이진식 (a0, a1, ...ak)을 사용하므로, a=a020 +a121 +...+ak2k가 됩니다. 이는 임의의 x1, ... , xkЄZ 을 생성하여 블라인드 계수로 사용되며, 코멘트를 정의하고, 각 ai에 대해 Ci = xiG + ai2iH를 정의하고, 공개 캐 {Ci , Ci - 2iH}를 생성합니다. 여기서 공개 키 중 하나는 확실히 xiG와 동일합니다: ai=0,Ci=xiG+0H=xiG일때, ai = (소스에 숫자가 누락된 경우), Ci−2iH=xiG+2iH−2iH=xiG. 즉, 블라인드 계수 xi는 항상 {Ci , Ci - 2iH}중의 하나에 대한 비밀 키입니다.

수수료 f의 커미트먼트는 블라인드 계수의 마스킹 효과 없이 계산되며 방정식은 C(f)= fH입니다. zG의 정확성을 검증하기 위해 네트워크는 아래 식을 계산합니다. QURAS를 적용할 수 있는 비즈니스 활용 사례:

QURAS 내에서 링 서명을 활용하는 방법은 익명으로 코인을 보내는 방법과 계약의 토큰을 익명으로 송금하는 2가지가 있습니다.
QURAS 플랫폼의 적용 범위는 링 서명의 특성으로 인해 다음과 같은 파일에 국한되지 않습니다:

전자상거래 (E-Commerce): 인터넷상의 전자 정보 통신을 통해 상품 / 서비스를 판매 / 구매할 때 사용자의 개인 정보가 필요합니다. 이러한 거래를 할 때는 사용자의 개인 정보를 보호하는 것이 중요합니다. 링 서명을 사용하면 사용자의 신원을 익명으로 확인할 수 있습니다.

전자 투표 (E-voting): 전자 투표는 전자적으로 수행되는 투표 행위입니다. 링 서명 기술은 전자투표에 적용해 유권자의 프라이버시를 보호하고 본인 확인을 할 수 있습니다

입찰 (Bidding): 입찰은 어떤 계약자가 판매 / 구매 및 계약 계약에서 가장 유리한 조건을 제안 하는지를 결정하는 방법입니다. 이 과정에서 여러 판매자는 서비스 내용과 가격이 포함 된 문서를 선택하기 전에 제출합니다. 링 서명 기술을 사용하면 입찰자 및 입찰 가격과 같은 정보를 숨길 수 있는 입찰 시스템을 개발할 수 있습니다.

IoT: IoT(Internet of Things, 사물 인터넷)는 여러 가지 "물건"이 인터넷에 연결되어 있어 서로 통신하고 서로를 제어 할 수 있도록 연결되어 있을 뿐 아니라 인터넷과 연결되어 있습니다. 이 경우 인터넷에서는 장치 식별 확인, 익명 메시지 통신 및 동의가 필요하므로 관리자와의 링 서명이 이 분야에 가장 적합합니다.

NFC: NFC(Near field communication, 근접 무선 통신)은 수 센티미터의 짧은 통신 영역에 대해 단파 HF 대역 (13.56 MHz)를 사용하는 특성을 갖는 단거리 무선통신 기술로 개인 식별 기술을 하는 유형입니다. NFC 칩을 스마트폰과 같은 소형 장치에 장착함으로써 다른 NFC 호환 장치와 통신을 가능토록 하는 기능을 갖게 되었습니다.

QURAS 플랫폼의 익명 기능을 사용하면 NFC 통신에서 기기 식별 정보를 확인하고 기기의 프라이버시를 유지할 수 있습니다.위의 모든 영역에서 QURAS 플랫폼을 사용하여 프라이버시를 보호할 수 있습니다.

현재 사용되는 zk-SNARK 기술은 높은 CPU 사용량을 요구하는 증명 생성 알고리즘 실행을 위해 사용됩니다. 컴퓨터가 적절한 메모리와 자원을 가지고 있다면 영지식 증명을 만드는 데 최대 몇 분 정도 걸릴 수 있습니다. 그러나 대부분의 경우 zk-SNARK를 생성할 때 보호된 단일 거래를 실행하려면 매우 집약적인 계산 프로세스가 필요하며, 대부분의 경우 3GB 이상의 RAM이 필요합니다. 즉, 이 기술은 모바일 기기에도 적용할 수 없습니다. QURAS 팀은 zk-SNARK 알고리즘에 대한 연구를 신속히 진행하기 위해 노력하고 있습니다.

향후, 증명 생성 시간과 공개 키 크기를 줄이는 것을 목표로 하는 BLS12-381이라는 타원 곡선을 채택할 계획입니다. 이 기술은 검증 시간을 기존보다 80%, 메모리 사용량을 98% 줄일 수 있게 합니다. 이것은 보호된 거래가 극히 적은 자원을 가진 모바일 장치와 컴퓨터에 의해 실행될 수 있음을 의미합니다.

모바일 월렛 제공업체는 물론 외환도 익명 주소/거래에 대한 전폭적인 지원을 구현할 수 있게 됩니다. 이 수준의 zk-SNARK 성능이 확보되면 IoT 업계와 IoT 하드웨어에서 보안 거래 활용이 가능해집니다. 64비트 Raspberry Pi와 같은 새로운 기기는 QURAS 보호 거래를 실행하고 IoT에 완전한 프라이버시를 부여할 수 있습니다.

QURAS는 영지식 증명이 구축된 하드웨어를 거래가 서명된 하드웨어와 분리할 수 있도록 키의 권한을 분리합니다. 이렇게 하면 안전성이 이전보다 높아집니다

Bootle et la의 기술을 바탕으로, 업데이트는 Bulletproof를 구현하고 Fiat-Shamir 휴리스틱 (발견적) 방법을 사용하여 비-대화형 영지식 증명을 제공 할 계획입니다. 이렇게 하면 신뢰할 수 있는 설정이 필요하지 않으므로 서명 생성 시간과 비용을 줄일 수 있습니다. 또한 기존 링 서명이 링 멤버의 신원을 밝히지 않고도 서명할 수 있기 때문에 서명자의 신원을 추적하는 경우에 추적 가능 / 신원 기반 링 서명 방법을 구현할 계획입니다.
실제 사용 사례를 고려할 때 문제가 발생하면 서명자의 신원을 추적하거나 공개해야 하는 경우가 있습니다