QURAS使用名为“zk-SNARK”的零知识证明 。使用zk-SNARK可以实现交易和智能 合约的完全隐私(匿名)。 zk-SNARK是“Zero-Knowledge Succinct Non-Interactive Argument of Knowledge”的缩写。 Succinct简洁意味着消息大小远小于实际执行的 计算量。 Non-Interactive 非交互式意味着可以在不需要验证者和证明者之间实时通 信的情况下进行验证。Argument of Knowledge知识论证是指通过计算进行知识验 证。即使zk-SNARK技术可用于隐藏发送人、汇款和金额信息，包括三种主要算法可 以检查交易:

G: 密钥生成算法，从特定秘密值R和函数C生成证明密钥(pk)和 验证密钥(vk)，其 中(pk，vk)= G(R，C))

P: 证明者生成证明的算法，从证明密钥(pk)，需要验证的信息(x)和函数C的输入(h) 生成证明prf，其中prf = P(pk，X，h))

V: 验证者进行证明验证的算法，通过验证密钥(vk)，函数C的输入(h)和证明prf来验 证证明者提供的信息是否正确，V(vk，h，prf)=true或false。目的是验证者在不必 询问证明者的情 况下，以较少的计算在短时间内执行验证工作。

zk-SNARK的执行需要以下步骤：

计算 算术电路 R1CS QAP zk-SNARK

算术电路

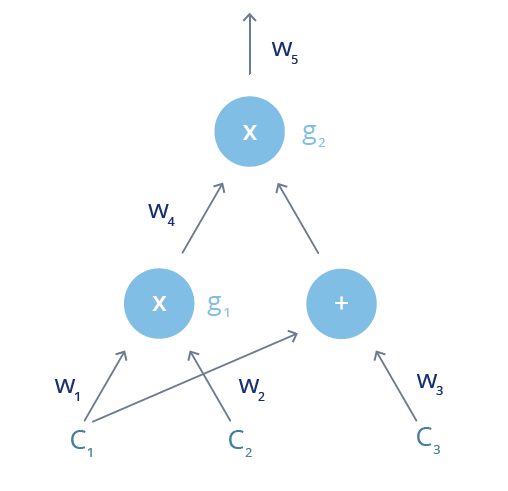
为了将交易有效函数转换为数学表达式，逻辑步骤首先被分解为尽可能少的操作， 以创建“算术电路”。假定A需要向B证明他知道c1，c2，c3，使(c1·c2)·(c1+c3)=7，按 照惯例，c1，c2，c3需要对B保密，证明A知道c1，c2，c3，第一步是将数学公式转 换为算术电路。

算术电路以门计算运算符表示，看起来像连接闸门、加法和乘法的导线。该电路看 起来像下面的数学公式:

R1CS:

接下来，运算电路将被转换为一阶约束系统(R1CS)。R1CS是一组包含三个向量 (a，b，c) 的序列。R1CS的解决方案需要满足向量s，其中s需要满足方程s.a * s.b - s.c = 0。 s表示所有输入向量，或换句话说，[C1，C2，C3，S1 ，S2，S3]。由于这 可以用相同的方式表示加法门，通过添加虚拟变量“1”，s向量 将转换为[1，C1，C2 ，C3，S1，S2，S3]。这三个闸门如下:

a=[0,1,0,0,0,0,0]
b=[0,0,1,0,0,0,0]
c=[0,0,0,0,1,0,0]

a=[1,0,0,0,0,0,0]
b=[0,1,0,1,0,0,0]
c=[0,0,0,0,0,1,0]

a=[0,0,0,0,1,0,0]
b=[0,0,0,0,0,1,0]
c=[0,0,0,0,0,0,1]

QAP:
下一步是将此R1CS转换为QAP(二次运算程序)格式。上述三个向量组可以表示为数 组：a(x)，b(x)，c(x)，由x表示。存在多项式表达式，其中P(x)= sa(x)* sb(x) - sc(x) ， P(x)= T(x)* H(x)，意味着P(x)= T( x)* H(x)可被证明，可以验证上述数学公式。通 过 将sa(x)定义为L(x)，将sb(x)定义为R(x)，将sc(x)定义为O(x)，需要证明的数学公 式 可以重写为L(x)* R(x)-O(x)= T(x)的* H(x)。

1. A根据上述方法选择多项式L，R，O，H。
2. B选择随机点s并计算E(T(s))。
3 .A基于B发送的(E(s)，E(s2),...)计算E(L(s)),E(R(s)),E(O(s)),E(H(s))
sent from B.
4. B验证E(L(s)* R(s)-O(s))= E(H(s)* T(s)).。

此处应用了称为同态加密的理论。同态加密是定义为x或E(x)的数满足以下性质的函 数:

对于几乎所有的x，一旦找到E(x)就很难找到它。如果输入不同，其输出也将不同。 这意味着，在x ≠y的情况下，E(x)≠ E(y)。如果有人知道E(x)和E(y)，就能够使用 E(x)和E(y)E来计算(x + y)。这意味着，虽然隐藏了x和y，但可以证明其他人可能知 道x + y的结果。

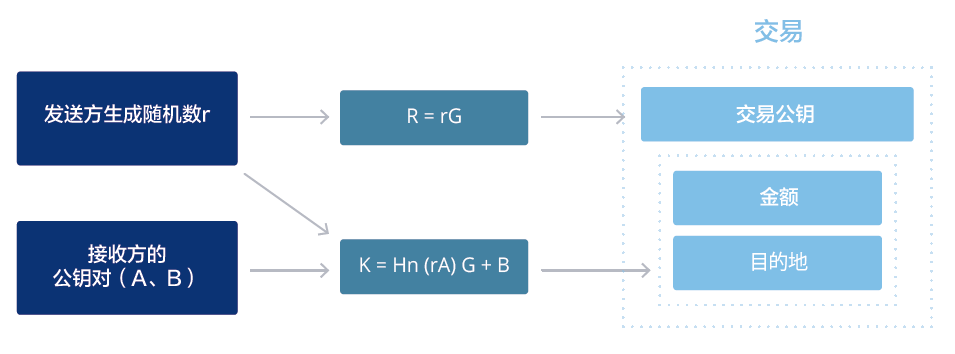
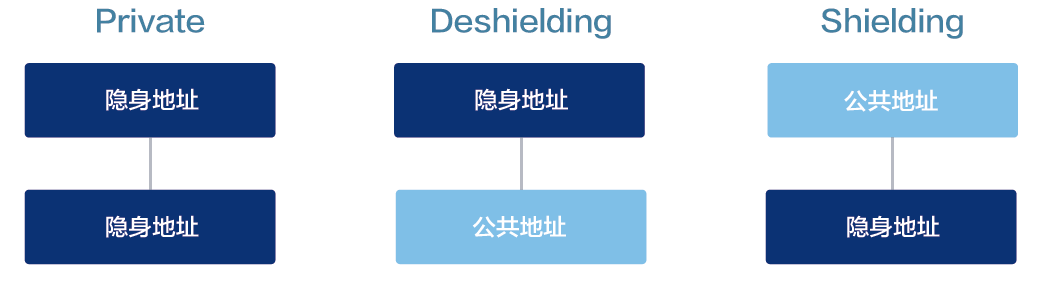
zk-SNARK技术可用于QURAS平台上的匿名交易。在发送/接收资金期间，zk-SNARK 技术可以实现三种类型的交易:1)隐私(隐身地址到隐身地址)，2)去屏蔽(隐身地址 到 公开地址)和3)屏蔽(公开地址到隐身地址)。
屏蔽(从公开地址到隐身地址)
这意味着可以使用ZK-SNARKS加密交易详细信息，包括发送人、接收人和交易金 额。使用它可以在不知道共识节点中的用户私钥的情况下验证加密交易是否正确。

zk-SNARK交易

也就是说，使用ZK-SNARKS有两个新概念 - Commitment（承诺）和Nullifier（废弃 值） 。假设在QURAS区块链中 加密的剩余余额显示为Note，从比特币来看，Note 的概念可以看作是UTXO的类似 概念。不同之处在于Note是加密的，并且不像UTXO 那样具有透明度。以下将说明验证者如何验证Note。Commitment可以被视为 Unspent Note，而对于比特币，它与Unspent UTXO相同:
Nullifier可用于防止重复付款，但它们是Spent Note。作为交易输入的引用发布，将 其哈希设置为废弃值。
交易输出是它们的哈希值，它们的Commitment将在区块链中公布。在QURAS区块 链中，首 先生成以下密钥以使用zk-SNARKS:

VAmount_Old和VAmount_New的值不能为1或更高。
如果这两个值均为1或更高，则该交易被视为失败。
此外，ZK-SNARKS验证、通过JoinSplit证明和ZK-SNARK验证密钥完成。如果为 True，则认为交易成功。如果不是True，则该交易被视为失败。

加密交易应包括至少一个JoinSplit项。当JoinSplit构建时，密钥对需要在第 一阶段产生，为签名密钥(JoinSplitSig)来验证JoinSplit。JoinSplit生成完成 后，JoinSplitPrivKey用于签名JoinSplit的主体。在此之后，在交易中输入 JoinSplitSig，以生成区块链广播的交易。

( 假设Note承诺树的深度是MerkleDepth。)
在Quras区块链中，可以根据Merkle树的Auth Path理论验证Markle树的根值和正确 性。

余额如前所述，匿名交易中存在JoinSplit项。JoinSplit项目中的VAmount_old表示从透明 余额池中拉出代币。VAmount_new表示将代币放入透明余额池的行为。用户只需通 过JoinSplit的VAmount_old和VAmount_new 查看QURAS区块链整个透明余额池的剩 余余额 。无法查看其他适用帐户的余额。

JoinSplit项不止一个，当一个交易被放入区块链时，其JoinSplit的承诺被添加到区块 链的Note Commitment Merkle Tree中。
此外，JoinSplit的废弃值将在区块链中注册。注册匿名交易时，如果Tx的废弃值已 经在区块链中注册，则交易将被识别为双花，并返回到区块链而不会被注册两 次。
在废弃值计算中，即使在Note中输入了随机字符串，其废弃值也会不同。这样，废 弃值可以防止双花。

智能合约意味着可以验证自发计算。除了使用zk-SNARK技术来保护代币交易隐私之 外，还可以执行可验证和匿名的计算。

证明生成和zk-SNARK的验证，需要从特定秘密值R和函数C生成的证明密钥(pk)和验 证密钥(vk)。该R称为有毒废物。QURAS的有毒废物将来自可信赖的多方并完全处置 掉。

环签名是QURAS中使用的第二种匿名技术。QURAS使用包含管理员的环签名技术， 因为签名后出现问题时需要识别签名。

签名者披露请求有两种类型:1)签名者向第三方或当事人证明签名的签名者是自 己，2)可信任的管理员放弃给定签名的匿名性，并在不需要签名者配合的情况下识 别签名者。

在上面，包含使U T_j^f(0) mod p成立的j的Uj，就是签名者。

QURAS 内的环签名交易

一次性地址：

QURAS区块链环签名的 一次性地址包括从两个椭圆曲线生成的密钥对((a，A)和 (b，B))。地址由(A，B)生成 。 (a，b)是一对私钥。 (a，B)是观察密钥。 有关资金转账，请参阅以下流程：
• 1，如果Alice想要向Bob汇款，首先，她将获取Bob的公钥(A，B)。
• 2，然后，Alice将选择随机数r，其中1 • 3，Alice将K设置为接收者，将值R = rG添加到交易数据，并将其发送到网络。接 收者将使用值R = rG来计算共享秘密，例如Diffie-Hellman。
• 4，Bob将接收数据，使用值R来计算aR = arG = rA以及K’= Hn(aR)G + B。由于aR = arG = rA则K’= K，当他看到地址时，他可以识别出这是他自己的地址。
• 5， Bob可以 使用 k = Hn(aR)+ b 来恢复一次性公钥K的密钥 。他将使用k重新签 署交易以进行汇款 。

环签名

金额承诺要在QURAS中隐藏环签名交易中的金额信息，请使用以下方法:
金额b的定义为C(b)= xG + bH，而x是致盲因子 。
如果存在输入a1 ， ... ， an和输出b1 ， ... ， bm 的交易， 观察者自然会期望 :

承诺是相加的，因此其总数也将为零:

这是为了确认使用网络交易的发送方没有发送比他或她之前收到的更多的代币。另 一方面，为了避免识别发送者的身份，承诺应该是非零的特定数字。

费用f的承诺是在没有盲因子的情况下计算的。等式是C(f) = fH。为了验证zG的正确 性，网络将计算以下等式:

可以应用QURAS的业务用例：
在QURAS中有两种使用环签名的方式：匿名发送代币和合约代币的匿名汇款。
由于环签名的特点，QURAS平台的应用范围包括但不限于以下领域:

电子商务: 在互联网上通过电子信息通信销售/购买商品/服务时，用户的个人信息是 必要的。在此类交易期间，保护用户的个人信息非常重要。通过使用环签名， 可以 匿名验证用户的身份。

电子投票: 电子投票是一种以电子方式完成投票的行为。环签名技术可用于电子投 票，保护选民的隐私，同时验证他们的身份。

招投标: 招标是确定哪个承包商在销售/购买和签订协议中提出最有利条件的方法。 在此过程中，几个卖家将在选择之前提交包含服务内容及其价格的文档。使用环形 签名技术可以开发出一种可以隐藏投标人和投标价格等信息的投标系统。

物联网: IoT(物联网)是一种机制，其中各种“事物” 连接到互联网(这意味着它们不仅 连接；而且像互联网一样连接)，以便它们可以相互通信和控制。在这种情况下，互 联网需要设备识别检查，匿名消息通信和协议送达，因此拥有管理员的环签名最适 合 该领域。

NFC: NFC(近场通信)是一种使用短距离无线通信技术的个人识别技术，其特征在于 短波HF频带(13.56MHz)用于几厘米的近场通信区域。通过将NFC芯片配备到诸如智 能 电话的小型设备，使其具有通过闭合而与其他NFC兼容设备通信的功能。QURAS 平台匿名功能的应用使得可以验证NFC通信上的设备身份，并且能够保持设备的隐 私。

对于上述所有领域，可以使用QURAS平台保护隐私。

目前使用的zk-SNARK技术用于执行校验生成算法，这需要高CPU使用率。如果电脑 具有适当的内存和资源，则可能需要几分钟才能构建零知识证明。
但是，在大多数情况下，在生成zk-SNARK时执行单个匿名交易需要极其大量的计算 资源，在许多情况下需要3GB或更高的RAM。
也就是说，这项技术无法应用于移动设备。QURAS团队正在努力加快研究zk-snark 算法的过程。
对于未来，我们计划采用名为BLS12-381的椭圆曲线，旨在减少证明生成时间和公钥 大小。
与以前相比，该技术可以将验证时间缩短80％，内存使用率降低98％。 这意味着匿名交易将可在具有极小资源的移动设备和电脑上执行。
移动钱包提供商以及交易所将能够实施对隐私地址/交易的全面支持。如果这种级别 的zk-SNARK性能可实现，则可以在物联网行业和物联网硬件中使用匿名交易。
诸如64位Raspberry Pi等新设备将能够执行QURAS匿名交易，并为物联网提供完全 隐私。

QURAS隔离密钥使用权限，以便构建零知识证明的硬件可以与签署交易的硬件隔 离。这样，安全性比以前更高。未来QURAS的环签名技术计划升级为完全匿名。除 剩余余额、发送方和接收方外，交易大小可以是匿名的。签名生成时间和费用也可 以降低，以提高效率。

QURAS环签名基于Bootle等技术，未来更新后计划实施Bulletproof，并使用Fiat-Shamir heuristic 提供非交互式零知识证明。
通过此更新，不需要可信设置，因此可以实现减少签名生成的时间和费用。
此外，该计划还将针对需要追踪签名者身份的情况，实现一种可追踪/基于身份的环 签名技术，因为现有的环签名允许环成员签名，而不必透露其身份。在考虑实际使 用案例时，如果出现问题，通常需要追踪或揭示签名者的身份。