QURAS uses zero-knowledge proof called “zk-SNARK”. Using zk-SNARK makes it possible to realize the complete privacy (anonymity) of transactions and smart contracts. zk-SNARK is an abbreviation of “Zero-Knowledge Succinct Non-Interactive Argument of Knowledge”. Succinct means message size is far smaller than the computation amount to be actually executed. Noninteractive means verification can be done without requiring communication between verifiers and approvers in real time. Argument of Knowledge refers to knowledge verification by computation. Even if the zk-SNARK technology is used to hide sender, remittance, and amount information, there are three major algorithms that still can check transactions:

G: Algorithm to generate a key (a proof key (pk) and a verification key (vk) are created from a certain secret value R and a program C, (pk, vk)= G(R,C) )

P: Proof is generated from proof key (pk), information to verify (X) and the input (h) to program C, prf = P(pk, X, h)

V: Verifier verifies the verification from the input (h) to program C, the proof (prf) and verification key (vk), verifies whether or not a verification is correct, “correct or incorrect” is returned. V(vk, h, prf) = True or False. The purpose of this is to perform verification work in a short amount of time with less computation without the approver having to question verifiers.

The execution of zk-SNARK requires the following steps:

Computation Arithmetic Circuit R1CS QAP zk-SNARK

Arithmetic Circuit

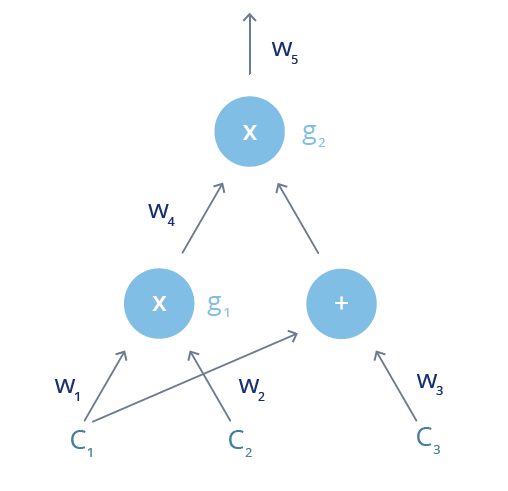
To convert transaction-effective functions to a mathematical expression, the logical steps are first broken down to the minimum operations as possible to create an “arithmetic circuit”. When c1, c2, c3 are known for A to be (c1 ˙ c2) ˙ (c1+c3)=7, the values of c1, c2, c3 are not indicated to B, and proving that c1, c2, c3 are known, the first step is to display a mathematical formula as an arithmetic circuit.

Arithmetic circuit is expressed in a gate calculation operator such as a wire that connects a gate, addition, and multiplication. The circuit looks like the mathematical formula below:

R1CS:

Next, the arithmetic circuit will be converted to the rank-1 constraint system (R1CS). R1CS is a sequence of a group of three vectors (a, b, c). The solution of R1CS needs to satisfy vector s, where s needs to satisfy the equation, s . a * s . b - s . c = 0. s. s . a * s . b - s . c = 0. s expresses all input vectors, or in other words, [C1 , C2 , C3 , S1 , S2 , S3]. Since this can express an addition gate in the same way, by adding a virtual variable, ”one”, the s vector will [one , C1 , C2 , C3 , S1 , S2 , S3]. These three gates are as follow:

a=[0,1,0,0,0,0,0]
b=[0,0,1,0,0,0,0]
c=[0,0,0,0,1,0,0]
a=[1,0,0,0,0,0,0]
b=[0,1,0,1,0,0,0]
c=[0,0,0,0,0,1,0]
a=[0,0,0,0,1,0,0]
b=[0,0,0,0,0,1,0]
c=[0,0,0,0,0,0,1]

QAP:
The next step is to convert this R1Cs to the QAP (Quadratic Arithmetic Programs) format. The above three-vector group can display the array, a(x), b(x), c(x), which is expressed by x. A polynomial expression exists in which P(x)=s.a(x) * s.b(x) - s.c(x) , P(x)=T(x)*H(x), meaning if P(x)=T(x)*H(x) is proven, the above mathematical formula can be verified. By defining s.a(x) as L(x), s.b(x) as R(x) and s.c(x) asO(x), the mathematical formula that needs to be proven can be re-written to L(x)*R(x)-O(x)=T(x)*H(x).

1. A select the polynomial expression L, R, O, H according to the above method.
2. B selects a random dot s and calculates E(T(s)).
3. A calculates E(L(s)),E(R(s)),E(O(s)),E(H(s)) based on (E(s) , E(s2),...) which was
sent from B.
4. B verifies E(L(s)* R(s)-O(s))= E(H(s)* T(s)).

The theory called homomorphic encryption is applied. Homomorphic encryption is defined as a function in which the number x, or E(x) satisfies the following natures:

For almost all x, it is hard to find it once E(x) is found. If an input is different, its output will be different as well. This means that, in the case of x≠y, E(x)≠E(y). If someone knows E(x) and E(y), he or she is able to use E(x) and E(y) E to calculate (x + y). This means that, while x and y are hidden, it can be proven that others may know the result of x + y.

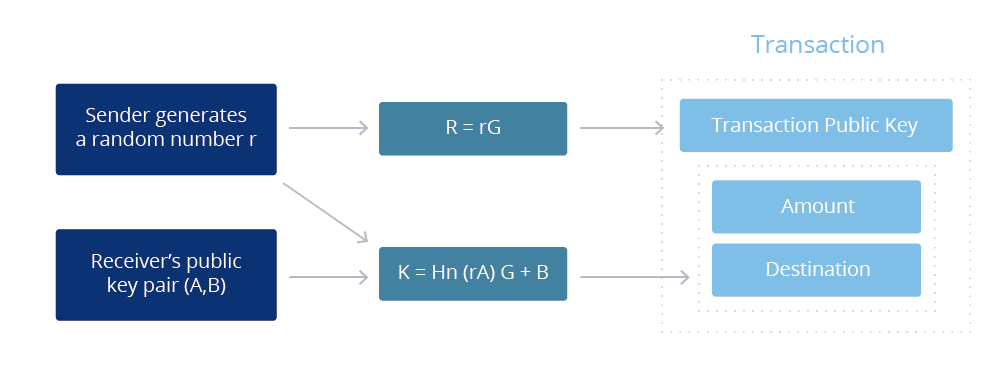
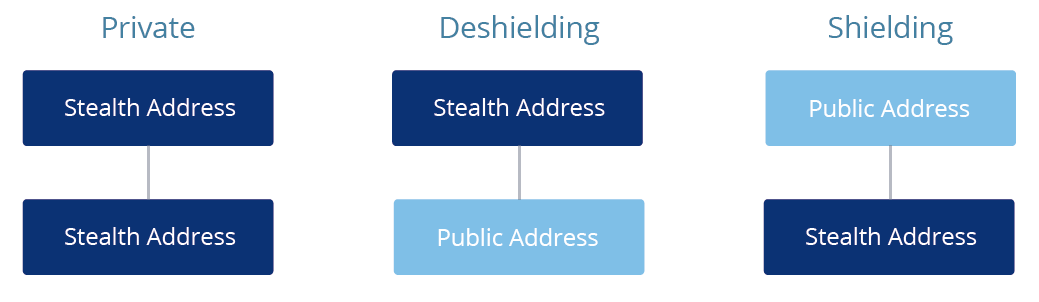
The zk-SNARK technology can be utilized to anonymize transactions on the QURAS platform. During sending/receiving funds, three types of transactions can be made possible by the zk- SNARK technology: 1) Private (stealth address to stealth address), 2) Desheilding (stealth address to public address) and 3) Shielding (public address to stealth address).
Shielding (from public address to stealth address)
This means encryption of transaction details including sender, recipient, and transaction amount by using zk-SNARKs. Using it makes it possible to determine if an encrypted transaction is correct without knowing its user’s private key in the consensus node.

Transaction’s zk-SNARK

That said, there are two new concepts in using zk-SNARKs – Commitment and Nullifier. Assuming a remaining balance that is encrypted in the QURAS blockchain is displayed as Note, from Bitcoin, the concept of Note can be seen as the similar concept of UTXO. The difference is that Note is encrypted and does not have transparency like UTXO does. The following will explain how Verifier verifies Note. Commitment can be considered as Unspent Note while for Bitcoin, it is the same as Unspent UTXO:
Nullifier is available to prevent duplicate payments, but they are Spent Note. References that are entered as transactions are published setting their hash as Nullfiler. Transaction Output is their Hash value and their Commitment will be published in the blockchain. In the QURAS blockchain, the following keys are generated first in order to use zk- SNARKs:

The values of VAmount_Old and VAmount_New cannot be 1 or higher. If these two values are all 1 or higher, the transaction is considered a failure. Also, though a JoinSplit proof and zk-SNARK Verify Key, zk-SNARKs verification is done. If True, the transaction is considered successful. If not True, the transaction is considered a failure.

Encrypted transactions shall include at least one JoinSplit item. When JoinSplit is built, a key pair needs to be generated during the 1st phase for a signature key (JoinSplitSig) to verify JoinSplit. Once JoinSplit generation is complete, JoinSplitPrivKey is used to sign on the body of JoinSplit. After this, JoinSplitSig is input in a transaction to generate a transaction for blockchain broadcasting.

(Assuming that the depth of Note Commitment tree is MerkleDepth.)
In Quras blockchain, it is possible to verify the root value and the correctness of Markle Tree based on Merkle Tree’s Auth Path theory.

As previously mentioned, there are JoinSplit items in an anonymous transaction. VAmount_old in JoinSplit item means pulling coin(s) out from a transparent balance pool. VAmount_new means an act to put coin(s) into the transparent balance pool. Users can simply check only the remaining balance of the QURAS blockchain’s entire transparent balance pool through JoinSplit’s VAmount_old and VAmount_new. The remaining balance of other applicable accounts cannot be viewed.

There is more than one JoinSplit item, and when a transaction is put into blockchain, its JoinSplit’s Commitment is added to the blockchain’s Note Commitment Markle Tree.
Also, JoinSplit’s Nullifier will be registered in the blockchain. When registering an anonymous transaction, if Tx’s Nullifier is already registered in the blockchain, the transaction will be recognized as double spend and returned to the blockchain without being registered twice.
In Nullifer computation, even if a random character string is entered in the Note, its Nullifier value will be different. This way, Nullifier prevents double spend.

Smart contract means a voluntary computation can be verified. In addition to using zk- SNARK technology to protect token transaction privacy, it is made possible to perform computations that are verifiable and anonymized.

The proof generation and the verification of zk-SNARK request a proof key (pk) and a verification key (vk) that are generated from a certain secret value R and the program C. This R is called a toxic waste. QURAS’ toxic waste will be generated from trusted multi-parties and completely disposed of.

Ring signature is the second anonymous technology used in QURAS. QURAS uses the ring signature technology with administrators since they are necessary to identify a signature in case a problem occurs after signing.

There are two types of signer disclosure requests: 1) A signer to prove to third party or parties that the signer of the ring signature is himself/herself, 2) A trusted administrator to surrender the anonymity of a given signature and identify the signer without the cooperation of the signer.

One-time address:

The ring signatures’ one-time address for QURASblockchain includes key pairs ((a,A) and (b,B)) that are generated from double-elliptic curves. The address is generated from (A,B). (a,b) is a secret key. (a,B) is a view key. For a fund transfer, please refer to the below process:
1, If Alice wants to send money to Bob, first, she will take Bob’s public key (A, B).
• 2, Alice will select a random r that satisfies 1 < r < N and calculate one-time public key K = Hn(rA) G+B.
• 3, Alice will set K as a recipient, add the value R=rG to a transaction data and send it to the network. The value R=rG will be used by the recipient to calculate shared secrets such as Diffie-Hellman.
• 4, Bob will receive the data, using the value R to calculate aR=arG = rA as well as K' = Hn(aR)G + B. Since aR=arG=rA and K'= K, when he sees the address, he can recognize that is his own address.
• 5, Bob can restore the secret key of the one-time public key K, using k=Hn(aR)+b. He will re- sign the transaction using k to carry out the money transfer.

Ring Signature

To hide amount information in the ring signature transaction within QURAS, the following methods are used:
The for the amount b is defined as C(b) = xG + bH while x is a blinding factor.
If there is a transaction with the input of a1,...,an and the output of b1,...,bm, an observer would naturally expect:

The commitment is additive, so its total will also be zero:

This is to confirm using the network that the transaction's sender did not send more coins than he or she received before. On the other hand, in order to avoid the sender’s identity being identified, commitment shall be a specific number that is other than zero:

The formula of the range proof is shown as below:

When there is a commitment for a, b, z and trying to use them to prove a + b = z, if a base filed is Z7 when a = 3, b = 2, z = 5, it can be applied to a = 4, b = 5, z = 2 (mod7). To resolve this issue, to solve for the amount a, the binary expression (a0, a1, ...ak)is used, so it will be a=a020 +a121 +...+ak2k. This will generate a random x1, ... , xkЄZ that will be used as a blind factor, define a commitment, Ci = xiG + ai2iH, for each ai and derive a public key {Ci, Ci-2iH} . Here, one of the public keys is clearly the same as xiG:
When ai=0,Ci=xiG+0H=xiG. When ai = 1, Ci-2iH = xiG + 2iH - 2iH = xiG. In other words, the blind factor xi is always a private key to one of the {Ci, Ci-2iH}.

The commitment of fee f is calculated without the masking effect by a blind factor. The equation is C(f)= fH. To verify the correctness of zG, the network will calculate the below equation:

Business use cases to which QURAS may be applied:
There are two ways of utilizing ring signature within QURAS: sending coins anonymously and the anonymous remittance of a contract’s tokens.
The application range of the QURAS platform is not limited to the following filed because of ring signature’s characteristics:

E-Commerce: When selling/buying commercial goods/services via electronic information communication on the internet, the user’s personal information is necessary. During such transactions, it is important to protect the users’ personal information. By using ring signature, a user’s identification can be verified anonymously.

E-voting: e-voting is an act of voting that is done electronically. The ring signature technology can be applied to e-voting to protect voters’ privacy while verifying their identification.

Bidding: Bidding is a method to determine which contractor proposes the most advantageous conditions in a selling/buying and contracting agreement. During the process, several sellers will submit a document that includes service contents and their prices before being selected. Using the ring signature technology makes it possible to develop a bidding system that can hide information such as bidders and bidding prices.

IoT: IoT(Internet of Things) is a mechanism in which various “things” are connected to the internet (which means they are not only connected; they are connected like the internet) so that they can communicate and control one another. In this case, the internet requires device identification check, anonymous message communication, and agreement-reaching, so the ring signature with administrators would be most suitable for this field.

NFC: NFC(Near field communication) is a type of individual identification technology that uses the short-distance wireless communication technology of which characteristics is to use the shortwaves HF band (13.56MHz) for several centimeters of the short communication area. By equipping a NFC chip to a small device such as a smartphone, it is made possible to have a function to communicate with other NFC-compatible devices by having them close. The application of QURAS platform’s anonymous function makes it possible to verify the device identification on the NFC communication and be able to keep the device’s privacy.

For all of the above area, privacy can be protected by using the QURAS platform.

Currently-used zk-SNARK technology is used to execute proof-generation algorithm, which requires high CPU usage. It may take up to few minutes to build zero-knowledge proof if a computer has appropriate memory and resources. However, in most cases, executing a single shielding transaction when generating zk-SNARK requires extremely intensive computation processes, which requires the RAM of 3GB or higher in many cases. That said, this technology cannot be applied to mobile devices. The QURAS team is trying to expedite the process of researching on the zk-SNARK algorithm. For the future, we plan to adopt an elliptic curve called, BLS12-381, aiming to reduce proof generation time and public key size. This technology will make it possible to reduce the verification time by 80% and memory usage by 98% compared to before. This means that shielded transaction will be executable by mobile devices and computers with extremely small resources. Mobile wallet providers, as well as exchanges, will be able to implement full support for shielded address/transactions. If this level of zk-SNARK performance becomes available, the use of shield transaction in the IoT industry and IoT hardware will be possible. New devices such as 64-bit Raspberry Pi will be able to execute QURAS shield transaction and give complete privacy to IoT.

QURAS segregates key’s permission so that the hardware in which zeroknowledge proof is built can be segregated from the hardware in which a transaction is signed. This way, the safety is higher than before.

Based on the technology of Bootle et la, updating is planned to implement Bulletproof and provide non-interactive zero-knowledge proof using Fiat- Shamir heuristic. By this, trusted set- up will not be required and therefore reducing signature generation time as well as fees can be realized. Also, the plan is to implement a traceable/identity-based ring signature method for a case of tracing signer’s identification being required as existing ring signature allows ring members to sign without having to reveal their identity. When considering actual use cases, in case of problem, it is often required to trace or reveal signer’s identity.